Hi, I’m Nathan. You may remember me from such posts as Logic Level Shifter for reading motor encoders and VNH5019 Additional Capacitor. I’m currently testing out the encoders on my 30:1 Metal Gearmotor 37Dx68L.
I wrote a test program to compare the PWM value against the motor speed measured by the encoder. I was expecting a linear relationship, but I found a logarithmic looking one. Below is a graph of my results, showing the average encoder counts per second against the Arduino PWM value (0-255).
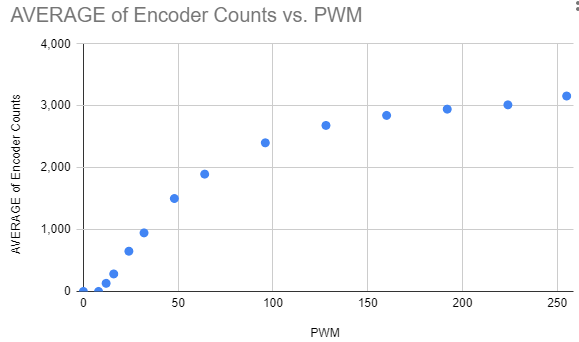
My questions are:
- Is my expectation of a linear relationship correct, or is the nonlinear relationship as expected?
- If my linear expectation is correct, can anyone see a problem with my test?
- Why is the top speed ~3150 counts per second instead of ~2640?
Any help or advice would be greatly appreciated.
I have the following connections between my components and the Arduino Nano 33 IoT microcontroller:
- D5 → IN1 on VNH5019
- D7 → IN2 on VNH5019
- D6 → PWM on VNH5019
- 3V3 → VDD on VNH5019
- GND → GND on VNH5019
- 5V → Encoder Vcc on motor
- GND → Encoder GND on motor
- D2 → Encoder A output on motor (via logic level shifter)
VIN on the VNH5019 is connected to a 3S 18650 battery, which is currently outputting 12.3V. As per my previous post, I measured 12V across the additional capacitor on the VNH5019.
Note that I also tried replacing the logic level shifter with a 1k/2.2k resistor voltage divider, but I got the same results.
My Arduino code is below:
const int ENCODER_A = 2;
const int ENCODER_B = 3;
const int IN1 = 5;
const int IN2 = 7;
const int PWM = 6;
const int MOTOR_SPEEDS[] = { 0, 8, 12, 16, 24, 32, 48, 64, 96, 128, 160, 192, 224, 255 };
const int MOTOR_SPEEDS_LENGTH = 14;
const int LOOP_MICROS = 1000000;
volatile int pulseCount = 0;
long loopEndTime = 0;
long measurementTime = 0;
int speedIndex = 0;
int speedLoopCount = 0;
void setup() {
pinMode(IN1, OUTPUT);
pinMode(IN2, OUTPUT);
pinMode(PWM, OUTPUT);
Serial.begin(2000000);
while (!Serial);
pinMode(ENCODER_A, INPUT_PULLUP);
pinMode(ENCODER_B, INPUT_PULLUP);
attachInterrupt(digitalPinToInterrupt(ENCODER_A), encoderPulse, RISING);
measurementTime = micros();
loopEndTime = micros() + LOOP_MICROS;
}
void encoderPulse() {
pulseCount++;
}
void loop() {
if (speedIndex >= MOTOR_SPEEDS_LENGTH) {
analogWrite(PWM, 0);
while (true);
}
int speed = MOTOR_SPEEDS[speedIndex];
speedLoopCount++;
if (speedLoopCount >= 15) {
speedIndex++;
speedLoopCount = 0;
}
//control speed
analogWrite(PWM, speed);
//control direction
digitalWrite(IN1, LOW);
digitalWrite(IN2, HIGH);
noInterrupts();
long now = micros();
int pulseCountValue = pulseCount;
pulseCount = 0;
interrupts();
long measurementInterval = now - measurementTime;
measurementTime = now;
Serial.print(speed);
Serial.print(",");
Serial.print(measurementInterval);
Serial.print(",");
Serial.println(pulseCountValue);
while(loopEndTime > micros());
loopEndTime += LOOP_MICROS;
}
