As part of my first effort to build an autonomous mobile robot platform “from the ground up” using the Netduino microcontroller I’ve spent a great deal of time reading about and exploring various strategies for obstacle avoidance. One of the issues I’ve been attempting to address is how to “turn” a moving robot in a determinate and repeatable manner to go around an object found to be in its path based on information returned by its on board sensors.
The robotic platform I am using for this project is the Pololu RP5 Robot Chassis. I chose it because it comes preassembled with two motors, gear trains and an AA battery pack at a very reasonable price. It is a very flexible platform in that one can add and stack a number of expansion plates to mount components on it. The current stage of construction incorporates the Netduino microcontroller, three Maxbotix LZ-EV0 ultrasonic sensors – one forward facing and one on each side facing outward at a 90 degree angle to the direction of travel, and a Sparkfun Serial LCD which is used to display data of interest during tests. The newest addition is an STMicroelctrionics LPY510AL dual axis pitch and yaw +/- 100/400 degrees/second MEMS gyroscope. This gyroscope is factory calibrated at 3v so it is perfectly suited for the Netduino. My main interest in the gyroscope is for detecting the yaw, rotation about the vertical axis passing through the center, when the RP5 chassis turns. I purchased the LPY510AL from Pololu, they sell it all ready mounted to a very nice breakout/carrier board with the “ST” recommended filtering and voltage regulating components in place; the gyro itself is a very tiny surface mount device, soldering it to a carrier looks to be more of a challenge than I’m interested in.
The first thing that one needs to understand about a MEMS gyroscope is that it reports the angular rate of rotation along each axis, i.e. how fast it is rotating, and not the angle that it has rotated about each axis. The results of attempting to derive a simple and straightforward method to calculate the angle of rotation about each axis is what I would like to present.
The “LPY5” reports angular rate on each axis as an analog voltage. When at rest, that is the gyro is not undergoing movement along any of its axis’, the spec sheet states that it will output a voltage level of 1.23v referred to as the “zero-rate level. The spec sheet also states that: “Zero-rate level of precise MEMS sensors is, to some extent, a result of stress to the sensor and therefore zero-level can slightly change after mounting the sensor onto a printed circuit board or after exposing it to extensive mechanical stress. This value changes very little over temperature and time.”
After soldering a header to the “LPY5” carrier board, plugging it into a breadboard and powering it up I checked the “zero-rate level” with a digital multimeter. I found the at rest voltage to be reported as 1.248v, certainly reasonable. Rotating the breadboard by hand in a counter clockwise direction, to the left, showed an increase in the output voltage representing a positive angular rate and rotating the breadboard in a clockwise direction, to the right, showed a decrease in the output voltage representing a negative angular rate.
I connected the “LPY5” to the Netduino 3.3v power, ground and an analog input pin. I also connected the Netduino AREF pin to 3.3v. I wrote a very simple class for the “LPY5,” which appears below. It should be noted that when the class is instantiated it is assumed that the gyroscope is at rest. Under this assumption I set the variable “atRestVref” to the reported “zero rate” voltage level to be used in calculating the angular rate when the gyroscope is rotating. The angular rate about the “Z” axis, yaw, at any given moment is returned by the “AngularRate()” function. I am using the “LPY5” over the range of +/- 400 degrees/sec. Over this range the gyroscope has a sensitivity of 2.5mv / degree / sec. Thus to calculate the angular rate one would use the formula:
((voltage output of “LPY5”) - (at rest output voltage output of “LPY5”)) / (2.5mv )/ degrees / sec.
If one works through this word formula carefully, it will be seen that the various units of the coefficients cancel out and one is left with a number which represents “degrees/second” which is the angular rate. It should also be noted that I am not concerning myself with what is referred to as “gyroscopic drift” or the need to do temperature compensation for the gyro because I am only going to be taking isolated readings at distinct points in time.
using System;
using System.Threading;
using Microsoft.SPOT;
using Microsoft.SPOT.Hardware;
using SecretLabs.NETMF.Hardware;
using SecretLabs.NETMF.Hardware.Netduino;
using Math = System.Math;
namespace PoluluRobot_010
{
class XZGyro
{
private Cpu.Pin inputPin { get; set; }
private AnalogInput analogInput { get; set; }
public double vRef { get; set; }
public double atRestVRef { get; set; }
public XZGyro(Cpu.Pin analogInputPin)
{
this.inputPin = analogInputPin;
this.analogInput = new AnalogInput(inputPin);
this.vRef = 3.3;
this.atRestVRef = (vRef / 1023.00) * (Convert.ToDouble(analogInput.Read().ToString()));
}
public double AngularRate()
{
return (((vRef / 1023.00) * (Convert.ToDouble(analogInput.Read().ToString())) - atRestVRef) / .0025);
}
}
}From a formal mathematical perspective one would find the actual angle of rotation around an axis of the gyroscope by integrating the angular rate over time. In reading through academic papers on robotic navigation with MEMS gyroscopes one will find some very elegant mathematics using quaternions, Heun’s method for integration, etc. However, I am not attempting to build an inertial navigation system and I’m really not sure of the Netduino’s ability to actually execute such complex algorithms in “real time.” At the same time if one thinks about integration conceptually, they will recall that it is about finding the area under a curve by taking the sum of the areas of a collection of rectangles which fill in the area under the curve. As the number of rectangles is increased to more closely fill in the space below the curve, the computed area becomes closer to the actual area. Perhaps an oversimplification but it should do.
My approach to the problem of deriving the actual angle of rotation from the angular rate reported by the gyroscope was that if I could get a large number of angular rates recorded over a period of time with the time duration of each sample being very small, I should be able to get a reasonable approximation of the angle of rotation for the gyroscope over the period of time. For any one sample the angle of rotation of the gyroscope is the (time duration of the sample) * (reported angular rate during of the sample). As the time duration of the samples becomes smaller the number of samples over any period of time increases and the results should become more accurate.
To establish a timer for the sample intervals I used "Stopwatch” class presented by another member of the Netduino forums. Since my specific goal was to control the turning angle of my robotic chassis I started out by attempting to define a “while” loop which would keep the chassis turning until a rotation of the desired number of degrees was completed. Inside the loop I would continuously take rate of rotation readings, multiply them by the duration of the reading to compute the angle of rotation for that sample and keep a running total of them. Once the running total of the angles of rotation was greater than or equal to the desired angle, the while loop ends. The result is the code below. Please note that the motorConroller class is a class I created for the Pololu Qik2s9v1 dual serial motor controller which is used to control the two motors in the chassis. The “TurnLeft” and “TurnRight” commands take an input parameter which represents a motor speed in the Pololu protocol.
using System;
using System.Collections;
using System.IO.Ports;
using System.Threading;
using Microsoft.SPOT;
using Microsoft.SPOT.Hardware;
using SecretLabs.NETMF.Hardware;
using SecretLabs.NETMF.Hardware.Netduino;
using System.Diagnostics;
namespace PoluluRobot_010
{
public class Program
{
static XZGyro yaw_gyro = new XZGyro(Pins.GPIO_PIN_A0);
static Stopwatch turnTimer = Stopwatch.StartNew();
static SerialIinput serialInput = new SerialIinput();
static InterruptPort interruptPort = new InterruptPort(Pins.ONBOARD_SW1, false, Port.ResistorMode.PullUp, Port.InterruptMode.InterruptEdgeLow);
static DualSerialMotorController motorController = new DualSerialMotorController();
static OutputPort crtlMaxbotixCenter = new OutputPort(Pins.GPIO_PIN_D7, false);
static OutputPort crtlMaxbotixLeft = new OutputPort(Pins.GPIO_PIN_D8, false);
static OutputPort crtlMaxbotixRight = new OutputPort(Pins.GPIO_PIN_D9, false);
static double currentTimeStamp = 0;
static double lastTimeStamp = 0;
static double angleTurned = 0;
static string ctrDist = "";
static string lftDist = "";
static string rgtDist = "";
static Int16 currRgtDist = 0;
static Int16 initRgtDist = 0;
public static void Main()
{
turnTimer.Start();
motorController.TurnLeft(50);
while (angleTurned < 90.0)
{
currentTimeStamp = turnTimer.ElapsedMilliseconds;
angleTurned = angleTurned + (((currentTimeStamp - lastTimeStamp) / 1000) * yaw_gyro.AngularRate());
lastTimeStamp = currentTimeStamp;
}
motorController.Stop();
turnTimer.Stop();
turnTimer.Reset();
lastTimeStamp = 0;
using (var s = serialInput)
{
s.ClearDisplay();
Thread.Sleep(50);
s.Print(angleTurned.ToString());
}Below is a screen shot of a portion of the list of values captured in the above “while” loop. The first column of numbers is the duration of the sample in seconds, the second column is the recorded angular rate – degrees/second. The last pair of numbers, outlined in red, show the total number of samples taken and the angle of rotation completed.
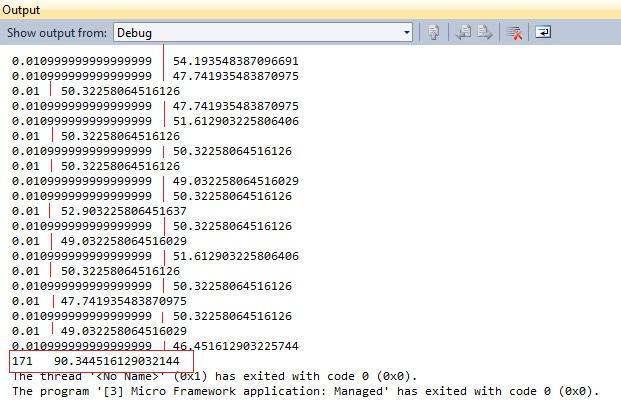
What is nice is that the robot rotates an almost perfect ninety degrees each time the loop is executed. Additionally, the logic was tested for rotations of 45 degrees and 180 degrees with equally accurate results. For rotations to the right one simple changes the while condition, in the case of a 90 degree right turn, to “while (angleTurned > - 90.0).” The results are also consistent over the full range of motor speeds I use, 30 – 70, and because they are based on the reported angular rate of the gyroscope over time they are independentof the charge level of the motor batteries and any wheel, or in the case of my particular robot chassis, tread slippage.

