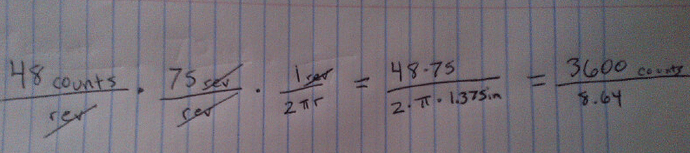Pololu Metal Gearmotor Encoder HELP!

Support A-Star and Orangutan
1

I have the 75:1 Metal Gearmotor 25Dx54L mm HP with 48 CPR Encoder, along with a Pololu Orangutan SVP 1284P. As you may know it already comes with the library to read the encoders. However, I have no past experience with encoders and I don’t know what does the value mean that the encoders is displaying on the Orangutan LCD screen. I would like to somehow calculate distance using the specs of the encoder and the value given back from the encoder. It is a 75:1 quadrature encoder, resolution of 48 cpr, 3592 counts/revolution, wheels I am using are 2.75inches or 6.985 cm with diameter of 21.944. I was wondering if someone could tell me a simple equation to hopefully calculate distance using these specs along with the value given back from the encoder.

HERE IS A SAMPLE OF MY CODE THAT I’M USING TO GET THE VALUE BACK FROM THE ENCODER:

#include <pololu/orangutan.h>
#include <math.h>
int main()
{
	svp_set_mode(SVP_MODE_ENCODERS);
	while(1)
	{
		set_m2_speed(75);
		//print("Encoder Count: ");
		print_long(svp_get_counts_ab());
		delay(400);
		clear();
	}
}
2

Hello.

In the future, please wrap your code in [code ] and [/code ] tags (without the inner spaces) to make it easier to read.

For reference, here is a link to the motor:
pololu.com/catalog/product/2275

The Orangutan SVP library functions you are using will read the number of encoder counts from the auxiliary processor. Encoder counts correspond to the total angle turned. The auxiliary processor measures both rising and falling edges of each encoder input, so you will get the full 48 counts per revolution of the motor shaft. There is a 74.83:1 gear ratio, so you have 75 revolutions of the motor shaft per revolution of the output shaft. Your wheels are circular, the diameter of a circle is 2piradius. You didn’t say the radius or diameter of your wheels; 21.944 doesn’t count because you forgot to say the units. If you had told us the radius of your wheels then I would be able to plug that into the formula to tell you how much distance your robot moves for every rotation of the output shaft.

In the end, you have a bunch of conversion factors and you just need to multiply them together:

(48 counts per revolution of motor shaft) * (74.83 revolutions of motor shaft per revolutions of output shaft) * (1 revolution of output shaft per 2pir distance)

The “per” basically means division. If you multiply all these conversion factors together and cancel out the units, you end up with a number whose units are simply counts per distance. Then you should verify that number by getting out a ruler and doing some actual experiments.

–David

3

Thanks! Sorry about the missing units. My wheels are 2.75 in == 6.985cm which result in a circumference of 21.944cm or 8.64 inches. So you are saying just multiply:

(48 counts/rev) * (75 rev /rev) * (1 rev / 2 * 3.14 * r = whatever units i decide ) = distance per one full wheel rotation

4

Not quite. You messed up your units at the very end. The “counts” are in the numerator and the “distance” is in the denominator, so the final units will be counts per distance.

–David

5

So it results to :

if i’m not mistaken all the rev’s should cancel out and just leave 3600 counts over 8.64 inches
3600 counts / 8.64 inches (i attached a pic of my calculations)
so this results to a wheel has traveled 8.64 inches for every full rotation or vice versa

calculation_encoder.png794×177 224 KB

6

Yes, that calculation looks good. It might be easier to think of it as 416.6 counts per inch. Before you go any further with your code, you should try rolling your robot about an inch and see if the value displayed on the LCD actually changes by about 400.

It would also help you keep things straight if you wrote something different for the two types of revolution. Perhaps srev for “shaft revolution” and orev for “output revolution”.

–David

7

YES IT WORKS THANKS!!! WOULD THIS EQUATION STILL BE RELIABLE IF THE ROBOT IS MAKING TURNS TO THE LEFT OR RIGHT, AND WOULD IT DECREASE THE COUNT IF THE ROBOT HAPPENS TO GO BACKWARDS?

8

Yes, the equation remains accurate, but please note that it is an equation for the total distance that the wheel has turned and it doesn’t take into account slipping of the wheel. It also won’t tell you where the robot is if the robot’s wheels move at different speeds (i.e. if the robot turns). Yes, the counts will decrease if the wheel turns backwards.

–David

9

Thanks David the advice cleared up a lot of confusion!!!